https://arxiv.org/abs/2403.10097
Introduction
Fine-tuningについての正則化の論文。
現在事前に訓練された深層学習モデルをTarget Datasetに正則化するのが一般的である。
この時重みは凍結するかどうかは、
この時うまく知識を転用できるときもあれば、Target DatasetにOverfittingしてしまうこともある。なので、うまく正則化手法を設定することでこれを防ぎたい。
いくつかの正則化手法はラベルやSource Datasetが必要であるが、CLIPなどの自己教師あり学習を分類のfine-tuningに使うとき(soruceやtargetデータの間でのタスクの種類が違う)はできない。また、そもそもSource Datasetが公開されていないとどうにもならない。
問題設定
ネットワークの使いたい特徴がある層(最後の層である必要はない)を入力として、線形層を1つだけ追加して、それの出力をモデルの出力としている。
定式化すると、
- クラス分類
- 訓練済み予測器 これの途中の層を入力として、を通して最終的な予測を得たい。
- のパラメタも学習できるようにする。は当然学習していく。
Related Work
Source Domainの情報を使わない正則化手法
- Feature Norm Penalty(FNP) 特徴抽出器の出力結果の値をL1/L2正則化する。
- 訓練済みのパラメタを初期で与えるが、凍結しないからbackboneのパラメタも変わるが、出力だけは当初から大きく変化しないようにする。なので、初期からのズレをL2ノルムを加える。
- DELTA の中間層における出力が、訓練済みのパラメタから多少なりとも変化していくが、それも変わらないようにしていく。よりもさらに中間層も気にしている感じ。
- Batch Spectral Shrinkage(BSS) ミニバッチ内の特徴ベクトル(backboneの中で取得したい層の値)を並べた行列の固有値に対する正則化。1から番目の固有値をできるだけ0にしたい。なぜならば、Fine-tuningというのは難しくないような簡単なタスクに特化させたいが、難しくないタスクに必要なデータの真の次元は高くないので、backboneの出力する特徴ベクトルが成す線形空間も高次元であってほしくないということ。
- Contrast-regularized Tuning(Core-tuning) 中間表現に対して対照学習を行う。つまり、同じクラスの潜在ベクトルは類似しやすくなるという制約を掛けたい。
- DR-Tune 新たに付けた線形層のがbackboneのの特徴ベクトルの分布を利用しても分類できるように。事前学習直後のパラメタでもうまく分類はできてほしいという正則化。(凍結せずに普通に学習は進めていくけど)
- RandReg 今回の手法の参考元。
Source Domainの情報を使う正則化手法
- Co-tuning Source DatasetとTarget Datasetは違うクラスに分類するが、それでもうまくDomain AdaptationすればTarget DomainにSource Domainのラベルから変換したPseudo Labelをつくれる。それをもとに、Target Datasetとともに学習する。
- Source Datasetも一応Pseudo Labelとしては学習をしているので、破滅的忘却を防ぎやすい。
- Unbalanced Optimal Transport(UOT) SourceとTargetを最適輸送を使ってDomain Adaptationすることで、Co-tuningと同じようにする。
RandReg
Source Domainの情報を使わない正則化手法である。目標は、特徴ベクトルと、あるランダムなベクトルの差の最小化を目指す。
ある分布を用意し、が正則化項である。つまり、ランダムに生成したベクトルとbackboneの中間表現があるランダムのベクトルに近づいてほしい。
ここで、はミニバッチごとに新たに設定されるので、毎回ランダムな位置に向けての距離で正則化をするという感じ。
勾配の式を展開してみると、FNPの正則化の項と、毎回ランダムな摂動の項(局所解に陥りにくくする)というような解になる。
欠点
- をうまく設定する必要があるし、平均や分散はDatasetによってAdhocである。
- ノイズ項が特徴ベクトルのノルムが小さいとノイズだけを拾って学びがちで、FNPよりも悪くなることもある。
- に特徴ベクトルを近づけるが、もしが小さすぎると、特徴ベクトルのノルムも小さくなって、結果的に特徴ベクトルの勾配も小さくなってしまう。
- 毎回のミニバッチから得られる特徴ベクトルの分布のEntropyが小さくなる。つまりミニバッチごとに似たり寄ったりする特徴ベクトルがふえてしまう。
- 極端な例だとすべての特徴ベクトルが決まった値とかになるって感じ。
- 手元のDatasetからEntropyを推測することはできる。ある特定の条件下では
- これ望ましくない?実際低次元の線形空間で情報が足りるならEntropyが小さくなってもいいが、情報が足りなくなるぐらい小さくなったらあかん。(ようはあんばい)
- 相互情報量で考える。全体のエントロピーからクラスごとのデータのエントロピーを引くことで得られる。
- 理想は全体のエントロピーは大きく、クラスごとのデータのエントロピーが小さいのがいい。
Proposed Method
RandSegの欠点を改善を試みた、AdaRandを提案した。
は1つの、何でもいい分布でよかった。しかし、AdaRandは。がクラスの数のぶんだけののガウス分布の混合ガウス分布によってなるとしている。混合の割合はClass Priorである。
最初は事前学習直後の特徴ベクトルの平均と分散ごとのクラスごとのガウス分布に代入する。
ミニバッチごとに、クラスごとの移動平均を更新していく。それを使って損失関数を計算し、を得ていく。
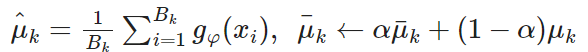
そして、クラス間はできるだけ離れるようにしてほしいが、同じクラスに所属してるデータはできるだけ近くなるように(を頑張って)したい。そのために以下の損失関数を使う。

は距離関数である。一項目はクラスについて、混合ガウス分布の期待値のパラメタをミニバッチの平均に近づけるようにしている。二項目は異なるクラスについて、その期待値ベクトルの距離が大きくなるようにしている。
合わせる目的のをランダム性を保ちつつも、その分布のパラメタ自体にはConstrastive Learningの知見(似たものは近く、違うものは遠く)を意識づけさせている。
実験結果
Fine-tuningでみんなより1%ぐらい良かった。
想定の通り、特徴ベクトル全体の空間の相互情報量はちゃんと大きくなるようにした。
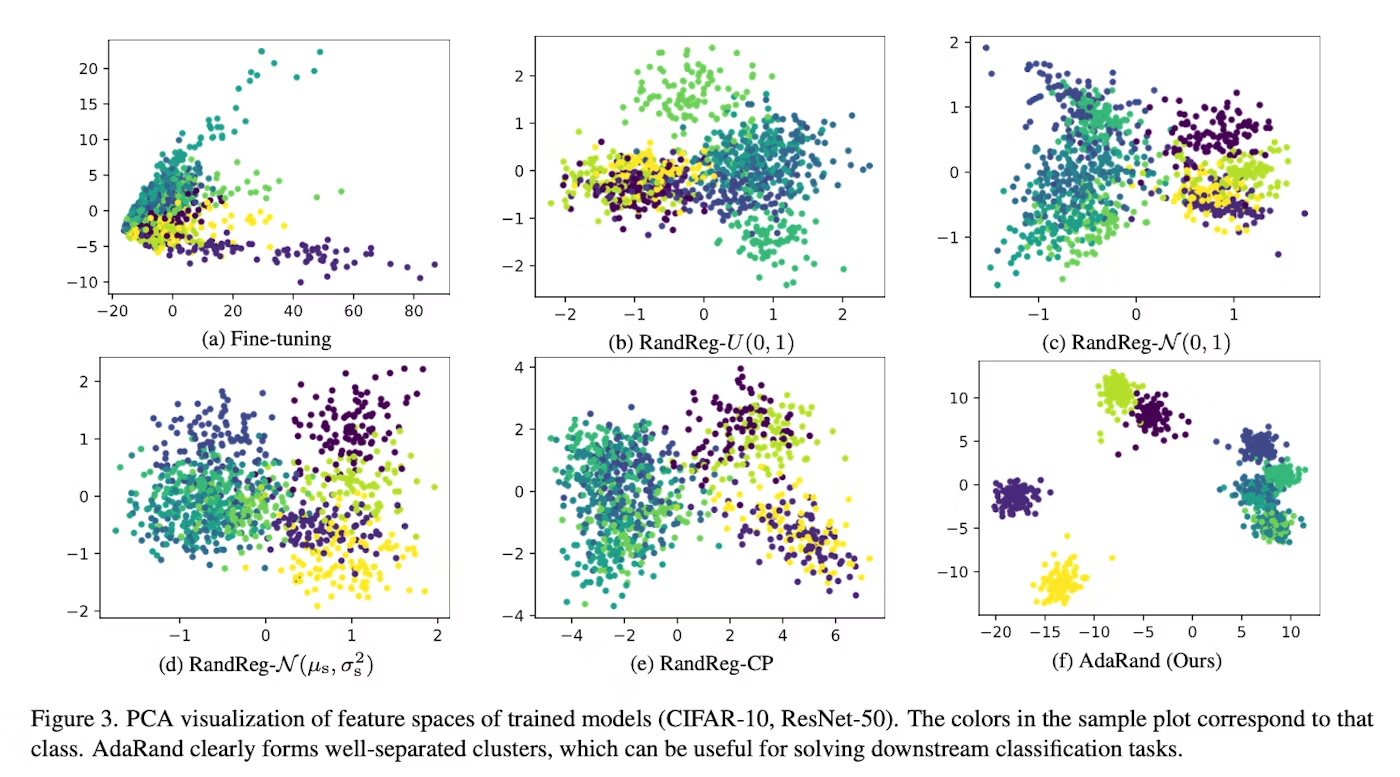
PCAで二次元に特徴ベクトルを投影してみたら、以下のようになった。